
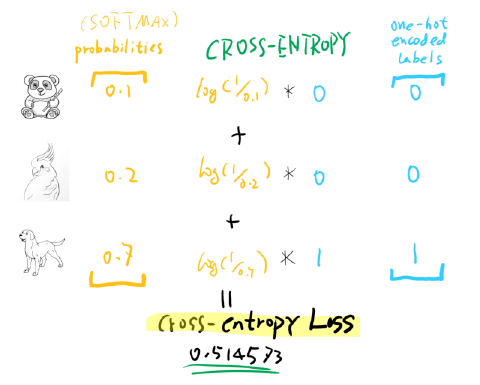
Notice the cross entropy of the output vector is equal to because our “true” distribution is a one hot vector: Where is the model output and is the index of the correct category. In classification models, often the output vector is interpreted as a categorical probability distribution and thus we have: This assumption allows us to compute the joint probability by simply multiplying the per example conditional probabilities:Īnd since the logarithm is a monotonic function, maximizing the likelihood is equivalent to minimizing the negative log-likelihood of our parameters given our data. Note that we are assuming that our data is independent and identically distributed. Since the dataset has multiple datum, the conditional probability can be rewritten as a joint probability of per example probabilities. Where is our dataset (a set of pairs of input and target vectors and ) and is our model parameters. Under the framework of maximum likelihood estimation, the goal of machine learning is to maximize the likelihood of our parameters given our data, which is equivalent to the probability of our data given our parameters: It’s important to know why cross entropy makes sense as a loss function. Therefore, if you don’t know what cross entropy is, there are many great sources on the internet that will explain it much better than I ever could so please learn about cross entropy before continuing. This post will be more about explaining the justification and benefits of cross entropy loss rather than explaining what cross entropy actually is. Not as much as I expected was written on the subject, but from what little I could find I learned a few interesting things. I thought it would be interesting to look into the theory and reasoning behind it’s wide usage. \newcommandĬross entropy loss is almost always used for classification problems in machine learning. The Benefits of Cross Entropy Loss - ML Review


 0 kommentar(er)
0 kommentar(er)
